Problems 6164 deal with the Vandermonde determinant that will play an important role in Section 3.7. The
Question:
Problems 61–64 deal with the Vandermonde determinant
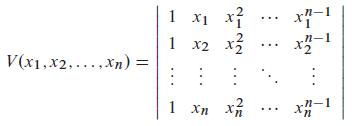
that will play an important role in Section 3.7.
The formulas in Problem 61 are the cases n = 2 and n = 3 of the general formula

Prove this as follows. Given x1, x2, and x3, define the cubic polynomial P(y) to be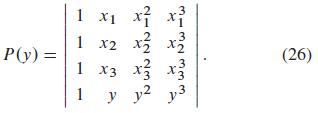
Because P(x1) = P(x2) = P(x3) = 0 (why), the roots of P(y) are x1, x2, and x3. It follows that
P(y) = k(y - x1)(y - x2)(y - x3),
where k is the coefficient of y3 in P(y). Finally, observe that expansion of the 4 x 4 determinant in (26) along its last row gives k = V(x1,x2, x3) and that V(x1, x2, x3, x4) = P(x4).
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Differential Equations And Linear Algebra
ISBN: 9780134497181
4th Edition
Authors: C. Edwards, David Penney, David Calvis
Question Posted:





