Problems 8 through 10 deal with the competition system in which c 1 c 2 = 8 < 9 = b 1 b 2 ,

Problems 8 through 10 deal with the competition system

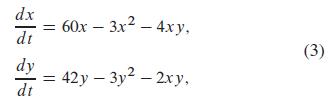
in which c₁c₂ = 8 1b₂, so the effect of inhibition should exceed that of competition. The linearization of the system in (3) at (0,0) is the same as that of (2). This observation and Problems 8 through 10 imply that the four critical points (0,0), (0, 14), (20, 0), and (12,6) of (3) resemble those shown in Fig. 9.3.13-a nodal source at the origin, a saddle point on each coordinate axis, and a nodal sink interior to the first quadrant. In each of these problems use a graphing calculator or computer system to construct a phase plane portrait for the linearization at the indicated critical point. Finally, construct a first-quadrant phase plane portrait for the nonlinear system in (3). Do your local and global portraits look consistent?

Show that the linearization of (3) at (20, 0) is u' = -60u - 80v, v' = 2v. Then show that the coefficient matrix of this linear system has the negative eigenvalue λ₁ = -60 and the positive eigenvalue λ₂ = 2. Hence (20 , 0) is a saddle point for the system in (3).

dx dt dy dt 60x - 3x 4xy, - - = 42y - 3y 2.xy, (3)