Repeat Problem 36, but this time assume that air resistance is proportional to instantaneous velocity. It stands to reason that the maximum height attained by the cannonball must be less than that in part (b) of Problem 36. Show this by supposing that the constant of proportionality is k = 0.0025.

Data from problem 36

Suppose a small cannonball weighing 16 pounds is shot vertically upward, as shown in the following figure, with an initial velocity v₀ = 300 ft/s. The answer to the question €œHow high does the cannonball go?€ depends on whether we take air resistance into account.

Suppose air resistance is ignored. If the positive direction is upward, then a model for the state of the cannonball is given by d²s/dt² = -g (equation (12) of Section 1.3). Since ds/dt = v(t) the last differential equation is the same as dv/dt = -g, where we take g = 32 ft/s². Find the velocity v(t) of the cannonball at time t.

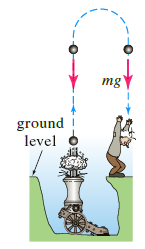
mg ground level