The current speed v_rof a straight river such as that in Problem 28 is usually not a constant. Rather, an approximation to the current speed (measured in miles per hour) could be a function such as v_r(x) = 30x(1 - x), 0 ‰¤ x ‰¤ 1, whose values are small at the shores (in this case, v_r(0) = 0 and v_r(1) = 0) and largest in the middle of the river. Solve the DE in Problem 30 subject to y(1) = 0, where v_s= 2 mi/h and v_r(x) is as given. When the swimmer makes it across the river, how far will he have to walk along the beach to reach the point (0, 0)?

Data from problem 28

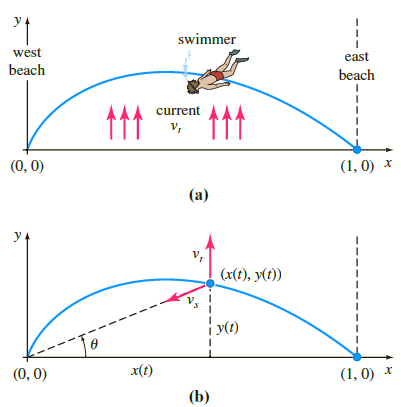
In the following figure (a) suppose that the y-axis and the dashed vertical line x = 1 represent, respectively, the straight west and east beaches of a river that is 1 mile wide. The river €“flows northward with a velocity v_r, where |v_r| = v_r mi/h is a constant. A man enters the current at the point (1, 0) on the east shore and swims in a direction and rate relative to the river given by the vector v_s, where the speed |v_s| = v_s mi/h is a constant. The man wants to reach the west beach exactly at (0,0) and so swims in such a manner that keeps his velocity vector v_s always directed toward the point (0, 0). Use figure (b) as an aid in showing that a mathematical model for the path of the swimmer in the river is

dy/dx = v_sy €“ v_rˆš(x² + y²)/v_sx.

Transcribed Image Text:

swimmer west east beach beach current v, (0, 0) (1, 0) x (a) y (x(t), y(t)) У) x(t) (0, 0) (1, 0) * (b)