The differential equation dy/dx = -x + (x 2 + y 2 )/y describes the shape of

The differential equation

dy/dx = -x + ˆš(x² + y²)/y

describes the shape of a plane curve C that will reflect all incoming light beams to the same point and could bea model for the mirror of a reflecting telescope, a satellite antenna, or a solar collector. See Problem 29 in Exercises 1.3. There are several ways of solving this DE.

(a) Verify that the differential equation is homogeneous (see Section 2.5). Show that the substitution y = ux yields

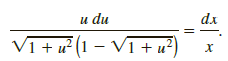
Use a CAS (or another judicious substitution) to integrate the left-hand side of the equation. Show that the curve C must be a parabola with focus at the origin and is symmetric with respect to the x-axis.

(b) Show that the ­first differential equation can also be solved by means of the substitution u = x² + y².

Transcribed Image Text:

u du VI + u (1 – V1 +u²) dx