Air is flowing through a venturi meter whose diameter is \(6.6 \mathrm{~cm}\) at the entrance part (location 1) and \(4.6 \mathrm{~cm}\) at the throat (location 2). The gage pressure is measured to be \(84 \mathrm{kPa}\) at the entrance and \(81 \mathrm{kPa}\) at the throat. Neglecting frictional effects, show that the volume flow rate can be expressed as

\[ \dot{V}=A_{2} \sqrt{\frac{2\left(P_{1}-P_{2}\right)}{ho\left(1-A_{2}^{2} / A_{1}^{2}\right)}} \]

and determine the flow rate of air. Take the air density to be \(1.2 \mathrm{~kg} / \mathrm{m}^{3}\).

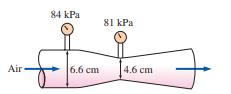
FIGURE P5-53

84 kPa 81 kPa Air- 6.6 cm 4.6 cm