Calculate the fan specific speed of the fan of Probs. 14–51 and 14–96 at the best efficiency point for the case in which the BEP occurs at 13,600 Lpm. Provide answers in both dimensionless form and in customary U.S. units. What kind of fan is it?

Data from Problem 14–96

Consider the fan of Prob. 14–51. The fan diameter is 30.0 cm, and it operates at ṅ= 600 rpm. Nondimensionalize the fan performance curve, i.e., plot C_H versus C_Q. Show sample calculations of C_H and C_Q at V̇ = 13,600 Lpm.

Data from Problem 14–51

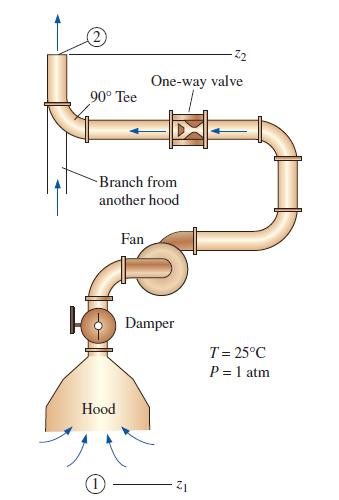
A local ventilation system (a hood and duct system) is used to remove air and contaminants from a pharmaceutical lab (Fig. P14–51). The inner diameter (ID) of the duct is D = 150 mm, its average roughness is 0.15 mm, and its total length is L = 24.5 m. There are three elbows along the duct, each with a minor loss coefficient of 0.21. Literature from the hood manufacturer lists the hood entry loss coefficient as 3.3 based on duct velocity. When the damper is fully open, its loss coefficient is 1.8. The minor loss coefficient through the 90° tee is 0.36. Finally, a one-way valve is installed to prevent contaminants from a second hood from flowing “backward” into the room. The minor loss coefficient of the (open) one-way valve is 6.6. The performance data of the fan fit a parabolic curve of the form H_available = H₀ – aV̇², where shutoff head H₀ = 60.0 mm of water column, coefficient a = 2.50 × 10^–7 mm of water column per (Lpm)², available head H_available is in units of mm of water column, and capacity V̇ is in units of Lpm of air. Estimate the volume flow rate in Lpm through this ventilation system.

FIGURE P14–51

Transcribed Image Text:

90° Tee -Branch from another hood Hood One-way valve Fan Damper T = 25°C P = 1 atm