Repeat Example 9–1 (gas compressed in a cylinder by a piston), but without using the continuity equation. Instead, consider the fundamental definition of density as mass divided by volume. Verify that Eq. 5 of Example 9–1 is correct.

Data from Example 1

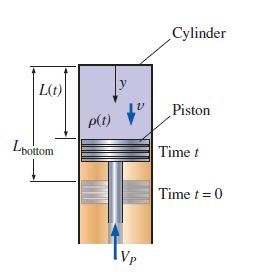
An air–fuel mixture is compressed by a piston in a cylinder of an internal combustion engine (Fig. 9–7). The origin of coordinate y is at the top of the cylinder, and y points straight down as shown. The piston is assumed to move up at constant speed V_P. The distance L between the top of the cylinder and the piston decreases with time according to the linear approximation L = L_bottom – V_Pt, where L_bottom is the location of the piston when it is at the bottom of its cycle at time t = 0, as sketched in Fig. 9–7. At t = 0, the density of the air–fuel mixture in the cylinder is everywhere equal to ρ(0). Estimate the density of the air–fuel mixture as a function of time and the given parameters during the piston’s up stroke.

Equation 5

FIGURE 9–7

Transcribed Image Text:

1 p(0) 1 - Vpt/L-bottom P² 1 1 - t* (5)