The generalized Bernoulli equation for unsteady flows can be expressed as

\[ \frac{P_{1}}{ho g}+z_{1}=\frac{V^{2}}{2 g}+\frac{1}{g} \int_{1}^{2} \frac{\partial V}{\partial t} d s+h_{L} \]

If the valve suddenly opened, the exit velocity will vary with time. Develop an expression for exit velocity \(V\) as a function of time. Neglect local losses.

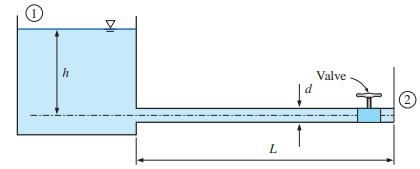
FIGURE P8-50

Transcribed Image Text:

h L d Valve 2