We approximate the flow of air into a vacuum cleaner’s floor attachment by the stream function

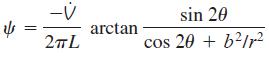
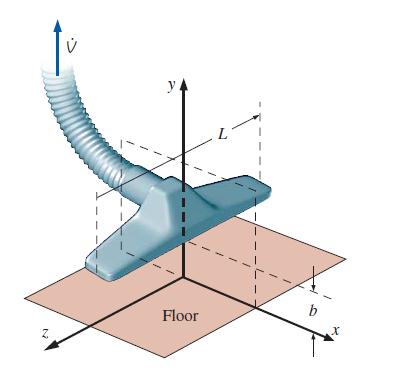
in the center plane (the xy-plane) in cylindrical coordinates, where L is the length of the attachment, b is the height of the attachment above the floor, and V̇ is the volume flow rate of air being sucked into the hose. Shown in Fig. P9–126 is a three dimensional view with the floor in the xz-plane; we model a two-dimensional slice of the flow in the xy-plane through the centerline of the attachment. Note that we have (arbitrarily) set ψ = 0 along the positive x-axis (θ = 0).

(a) What are the primary dimensions of the given stream function? 

(b) Nondimensionalize the stream function by defining ψ* = (2πL/V̇)ψ and r* = r/b. 

(c) Solve your nondimensionalized equation for r* as a function of ψ* and θ. Use this equation to plot several non dimensional streamlines of the flow. For consistency, plot in the range –2 < x* < 2 and 0 < y* < 4, where x* = x/b and y* = y/b.

FIGURE P9–126

Transcribed Image Text:

4 -V 2TTL arctan sin 20 cos 20+ b²/2²