As society searches for technical solutions to global warming, one approach to sequester carbon-dioxide rich greenhouse gases is to capture the CO₂within an adsorbent material at high pressure. An experiment designed to evaluate a candidate adsorbent material is presented in the figure below, which consists of a 10 cm × 10 cm slab with 100 cm²of exposed surface. A gas mixture of 10 mole% CO₂(species A) and 90 mole % N₂(species B) at 15.0 atm total system pressure and temperature of 200°C is contacted with a micro porous material designed to selectively adsorb the CO₂[rom the gas mixture. The partitioning of CO₂gas within the adsorbent is described by 

Q_A = K'c_A 

where Q_A is the amount of CO₂ adsorbed per unit volume of porous adsorbent (mol CO₂/cm³ adsorbent). c_A is the concentration of CO₂ in the gas phase within the porous adsorbent (mol CO₂/cm³ gas pore space). and K' is the apparent CO₂ adsorption constant (cm₃ gas/cm³ adsorbent). The experiment is conducted as an unsteady-state process where the total amount of CO₂ captured within the adsorbent is measured after a given time. Initially, there is no CO₂ adsorbed on the solid or in the pore space, and the process is considered dilute with respect to CO₂ in the gas phase. The diffusion process is modeled as semi-infinite sink for CO₂, with CO₂ flux given by 

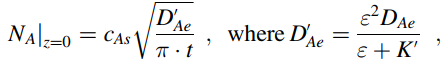
C_As is the molar concentration of CO₂ at the outer surface of the slab. In the above equation, D'_Ae is the apparent diffusion coefficient of CO₂ within the adsorbent material under conditions where the solute adsorbs onto the surface of the pores, which includes the following terms: apparent CO₂ adsorption constant (K'), the void fraction of the porous adsorbent (ε), and the effective diffusion coefficient of CO₂ within the solid under non-CO₂ adsorbing conditions (D_Ae). In the present system. K' = 1776.2 cm³/cm³, ε = 0.60, and D_Ae = 0.018cm²/s. After a total contact time of 60 min. what was the total mass of CO₂ captured by the slab? Consider that the slab acts as a semi-infinite sink for CO₂, and that convective mass-transfer resistances are eliminated so that C_As = C_Aˆž.

Transcribed Image Text:

DAe D'A where D'A | NAlz=0 = CAs ɛ + K' T·t