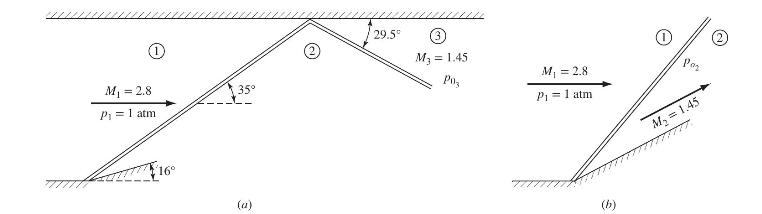
a. Consider the supersonic flow described in Example 4.10, where \(M_{1}=2.8, p_{1}=1 \mathrm{~atm}\), and \(M_{3}=1.45\). This flow is shown in Fig. 4.20a. Calculate the total pressure in region 3 where \(M_{3}=1.45\).

b. Consider the supersonic flow shown in Fig. 4.20b, where the upstream Mach number and pressure are the same as in part (a), i.e., \(M_{1}=2.8\) and \(p_{1}=1 \mathrm{~atm}\). This flow is deflected through the angle \(\theta\) such that the Mach number behind the single oblique shock in Fig. \(4.20 b\) is the same as that behind the reflected shock in Fig. \(4.20 a\), i.e., \(M_{2}=1.45\) in Fig. 4.20b. For the flow in Fig. 4.20b, calculate \(\theta\) and the total pressure in region \(2, p_{o_{2}}\).

Comment on the relative values of the total pressure obtained in parts (a) and (b).

Data From Example 4.10:

Consider a horizontal supersonic flow at Mach 2.8 with a static pressure and temperature of \(1 \mathrm{~atm}\) and \(519^{\circ} \mathrm{R}\), respectively. This flow passes over a compression corner with a deflection angle of \(16^{\circ}\). The oblique shock generated at the corner propagates into the flow, and is incident on a horizontal wall, as shown in Fig. 4.18. Calculate the angle \(\Phi\) made by the reflected shock wave with respect to the wall, and the Mach number, pressure, and temperature behind the reflected shock.

Figure 4.18:

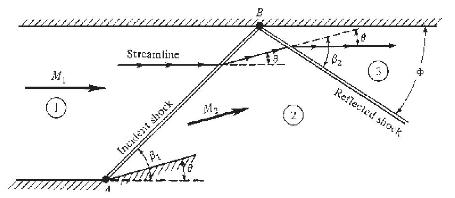
Figure 4.20:

Transcribed Image Text:

M Streamline Incident shock to Reflected shock