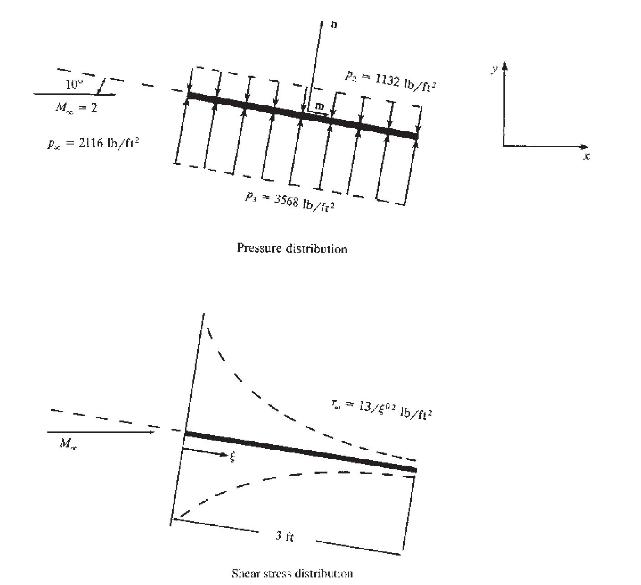
A flat plate with a chord length of \(3 \mathrm{ft}\) and an infinite span (perpendicular to the page in Fig. 1.12) is immersed in a Mach 2 flow at standard sea level conditions at an angle of attack of \(10^{\circ}\). The pressure distribution over the plate is as follows: upper surface, \(p_{2}=\) const \(=1132 \mathrm{lb} / \mathrm{ft}^{2}\); lower surface, \(p_{3}=\) const \(=3568 \mathrm{lb} / \mathrm{ft}^{2}\). The local shear stress is given by \(\tau_{w}=13 / \xi^{0.2}\), where \(\tau_{w}\) is in pounds per square feet and \(\xi\) is the distance in feet along the plate from the leading edge. Assume that the distribution of \(\tau_{w}\) over the top and bottom surfaces is the same. (We make this assumption for simplicity in this example. In reality, the shear stress distributions over the top and bottom surfaces will be different because the flow properties over these two surfaces are different.) Both the pressure and shear stress distributions are sketched qualitatively in Fig. 1.12. Calculate the lift and drag per unit span on the plate.

Figure 1.12:

Transcribed Image Text:

M 10 Mx = 2 Pxx = 2116 lb/ft 1 1 P = 3568 lb/ft Pressure distribution 3 it Shear stress distribution P. 1132 lb/ft = 13/8 15/ft