Consider a convergent-divergent nozzle of length \(L\) with an area-ratio variation given by \(A / A^{*}=1+10|x / L|\), where \(-0.5 \leq x / L \leq 0.5\). Assume quasi-one-dimensional flow and a calorically perfect gas with \(\gamma=1.4\).

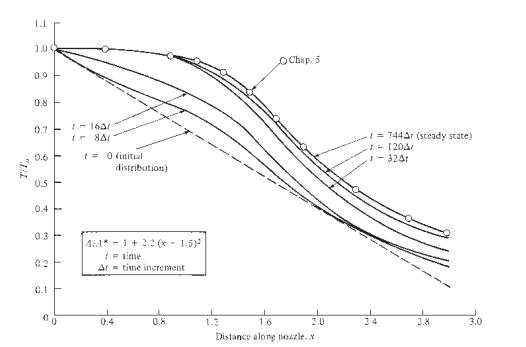
a. Write a computer program to calculate the variation of \(p / p_{o}, T / T_{o}\), \(ho / ho_{o}, u / a_{o}\), and \(M\) as a function of \(x / L\) by means of the time-dependent finite-difference technique. Plot some results at intermediate times, as well as the final steady-state results. Use Fig. 12.6 as a model for your plots.

b. On the same plots, compare your steady-state numerical results with the answers obtained from Table A. 1 

Figure 12.6:

Transcribed Image Text:

TIT 1.1 1.00 0.9 0.8 0.7- - 1641 18A 0.6 0.5 1 0.4- 0.3 02 C.1 T 70 (initial distribution) A1+22(x-1.5) [= time Artime increment 0 0.4 0.8 1.3 1.6 Chap. 5 t744Ar (steady state) 120A/ 1-32Ar 2.0 2.0 24 34 2.8 3.0 Distance along nozzle.x