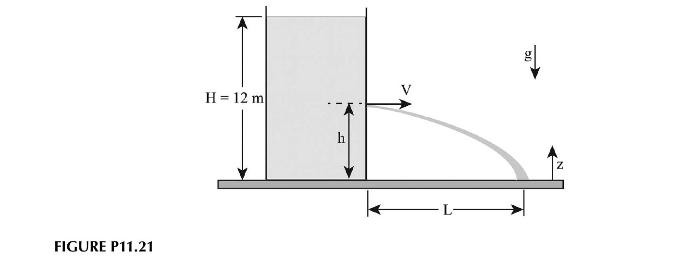
A hole is to be drilled into the side of the tank shown in Figure P11.21 so the liquid will travel the farthest horizontal distance, \(L\). You may assume the liquid height in the tank remains constant, the flow is inviscid and that gravity acts in the \(-z\)-direction.

a. What is the velocity of the water exiting the tank as a function of \(h\) ?

b. What are the velocity components of the exiting water and how do they change over time as the stream falls to the ground? You may assume that the water stream is traveling purely horizontally as it exits the tank at \(L=0\).

c. Using your answers from (a) and (b), determine an expression for the distance \(L\) as a function of \(h\), the velocity exiting the tank, and the height of liquid in the tank.

d. Where should the hole be drilled to insure \(L\) is a maximum? Why?

Transcribed Image Text:

H = 12 m h FIGURE P11.21 50