Biological organisms often couple extended surface transport with a facilitated mechanism to enhance mass transport. We have
Question:
Biological organisms often couple extended surface transport with a facilitated mechanism to enhance mass transport. We have talked about facilitated transport and have shown how we can model it using a chemical reaction. We can combine extended surface and facilitated transport by looking at a villus that employs a first-order chemical reaction within it to "enhance" the rate of nutrient absorption by reacting away species \(b\) within the fin itself. Figure P8.31 shows a diagram of the villus and the control volume. The physical parameters for the system are given below.
\[\begin{aligned}& L=0.0001 \mathrm{~m} \quad r=0.0005 \mathrm{~m} \quad D_{a b}=1 \times 10^{-7} \mathrm{~m}^{2} / \mathrm{s} \\& c_{b \infty}=100 \mathrm{~mol} / \mathrm{m}^{3} \quad c_{b b}=10 \mathrm{~mol} / \mathrm{m}^{3} \quad k_{c}=1 \times 10^{-4} \mathrm{~m} / \mathrm{s} \\& k^{\prime \prime}=1 \times 10^{-5}-1 \times 10^{-4} \mathrm{~m} / \mathrm{s} \quad K_{e q}=1\end{aligned}\]
a. What is the differential equation governing the concentration of \(b\) within the villus? The reaction is \(b \rightarrow c\) and is irreversible.
b. What is the fin number for this situation and how does it incorporate the reaction rate constant?
c. If the fin number for the case where reaction occurs is always larger than for the case of no reaction, what does that imply for the efficiency and effectiveness of the villus, the size of the villus, and under what possible circumstances could this facilitated case be better than the case where no reaction occurs?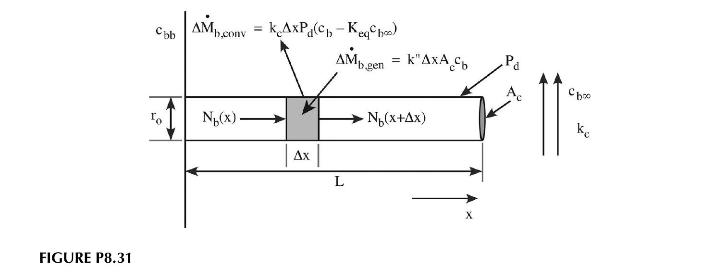
Step by Step Answer:






