Question:
In Section 2.4 we discussed the definition of a molar flux, in one dimension defined by
\[J_{a x}=v_{a x} c_{a}=-D_{a b} \frac{d c_{a}}{d x}\]
We can use this to define the velocity, $v_{a x}$. Given that the concentration profile in two media were measured at fit to the following equations, determine and plot the velocities in the two media as functions of position.
\[\begin{array}{ll}\text { Medium \#1 } & c_{a}=100 \exp (-4 x) \\\text { Medium \#2 } & c_{a}=100-9000 x\end{array}\]
Transcribed Image Text:
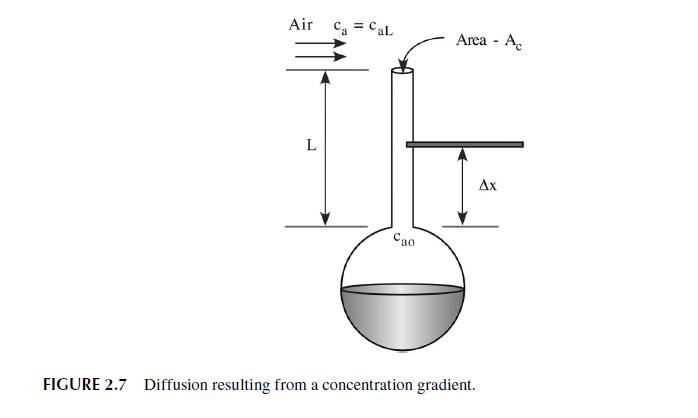
2.4 MASS TRANSPORT-FICK'S LAW OF DIFFUSION Long after Newton's Law, Fourier's Law, and Ohm's Law for electrical conductance were devel- oped, people were still uncertain about the movement of chemical species from one location to another. Adolf Eugen Fick (1829-1901), a physiologist, performed a series of experiments tying the flux of chemical species to a gradient involving the mole/mass fraction or concentration/density of chemical species. Figure 2.7 shows a simple apparatus designed to measure the motion, termed diffusion, of species a through a medium, b. An "infinite" reservoir of liquid a is attached to a long tube of small cross-sectional area, A. The temperature and pressure of the system are held such that the concentration of species, a, in the vapor is very low. At the inlet to the small tube, near the interface between vapor and liquid, the concentration of a is held constant at Cap. At the oppo- site end of the tube, pure air is blown by the opening to keep the concentration of a zero at the outlet. The small tube is fitted with ports so that a sensor can be inserted and used to measure the concentration of species a along the length of the tube. By varying the diameter of the small tube and the concentration of species a in the air stream, we find, as Fick did in his experi- ments in 1855, that the molar/mass flux of species a is directly proportional to the difference in








