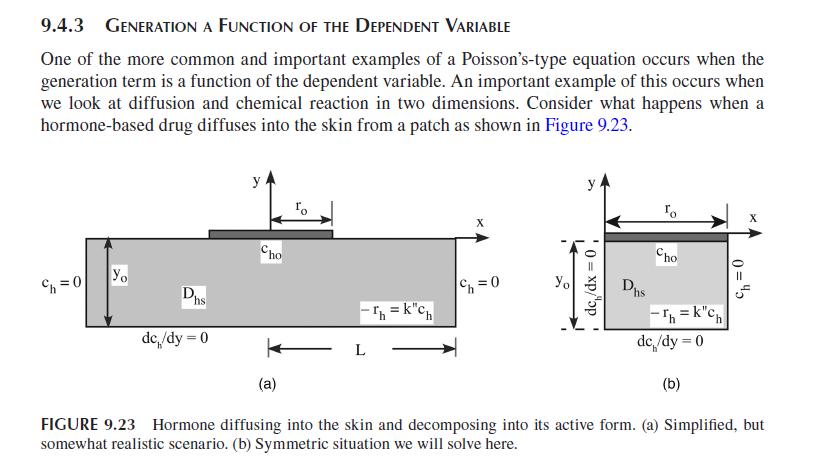
In section 9.4.3 we discussed the diffusion of a compound from a skin patch and its transport

Question:

In section 9.4.3 we discussed the diffusion of a compound from a skin patch and its transport and reaction once it entered the skin. We did a very simple example of this, not considering what happened beyond the boundaries of the patch. In this problem we would like to consider that process and look at a slightly modified problem that was too long for inclusion directly in the text. The problem is shown in Figure P9.30.

a. Derive the differential equations required to solve this problem over the entire half geometry from the symmetry point at \(x=0\) to the edge of the domain at \(x=L\). To do this, it will be helpful to separate the domain into two sections; one underneath the patch and the other to the right of the gray-dashed line.

b. What are the boundary conditions in each section?

c. What conditions must hold at the intersection between the two domains?

d. Solve the equations generically using the conditions in (b) and (c).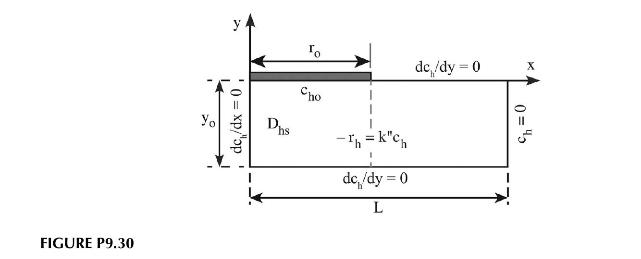 image text in transcribed