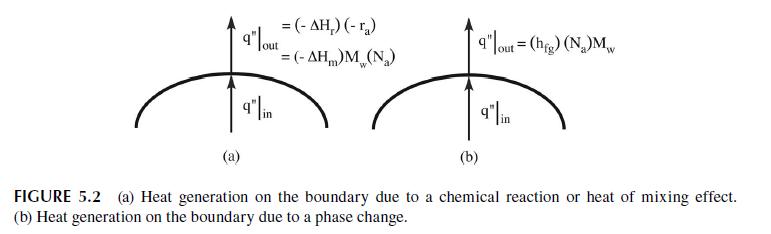
Reconsider the first example in the chapter regarding heterogeneous reaction on the boundary. In that example we
Question:
Reconsider the first example in the chapter regarding heterogeneous reaction on the boundary. In that example we used the simplest boundary condition for the reaction. In reality, the reaction occurs on the surface and we need species \(a\) to adsorb on that surface prior to reaction. In most instances of heterogeneous catalytic reaction, we relate the surface concentration to the bulk concentration using a Langmuir isotherm.
\[x_{a, \text { surface }}=\frac{K x_{a}}{1+K x_{a}}\]
a. Reevaluate the example, assuming that the reaction at the surface can be given by:
\[-r_{a}=k_{s}^{\prime \prime} x_{a, \text { surface }}\]
b. What is the mass flow rate to the surface if:
\[\begin{array}{lll}L=0.05 \mathrm{~m} & D_{a b}=1 \times 10^{-9} \frac{\mathrm{m}^{2}}{\mathrm{~s}} & A_{s}=7.85 \times 10^{-7} \mathrm{~m}^{2} \\K=10 & k_{s}^{\prime \prime}=1 \times 10^{-6} \frac{\mathrm{m}}{\mathrm{s}} & x_{a o}=0.5 \quad c_{t}=100 \frac{\mathrm{kg}-\mathrm{mole}}{\mathrm{m}^{3}}\end{array}\]
(to choose the value of the integration constant found in part (a), compare choices with the value obtained from equation (5.16).

Step by Step Answer:






