We can derive a theoretical form for the permeability in a simple situation. Consider the rectangular block
Question:
We can derive a theoretical form for the permeability in a simple situation. Consider the rectangular block of length \(L\), and sides of length \(s\), that has \(n\) cylinders of diameter \(d_{0}\), drilled through it as shown in Figure P2.3. For a given pressure difference between the two ends, the volumetric flow rate through one of the cylinders is given by:
\[\dot{V}_{i}=\frac{\pi d_{0}^{4}}{128 \mu} \frac{\Delta P}{L}\]
and through all of them by:
\[\dot{V}=\frac{\pi n d_{0}^{4}}{128 \mu} \frac{\Delta P}{L}\]
a. Derive an expression for the permeability, \(k\).
b. What is the void fraction of the material and can you express the permeability in terms of the void fraction?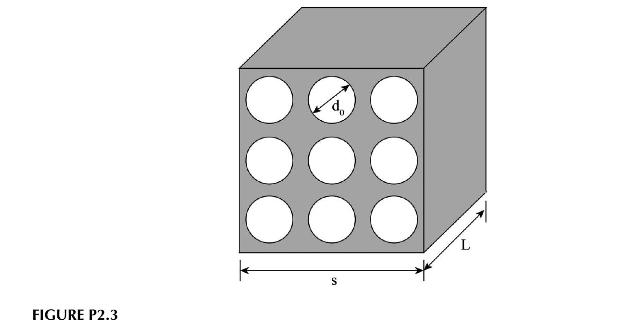
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





