Consider the rotating disk of Problem 6.16. A diskshaped, stationary plate is placed a short distance away from the rotating disk, forming a gap of width g. The stationary plate and ambient air are at T_∞ = 20 C. If the flow is laminar and the gap-to-radius ratio, G = g/r_o, is small, the local radial Nusselt number distribution is of the form

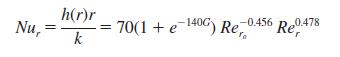
where Re_r = Ωr² /v [Pelle J., and S. Harmand, Exp. Thermal Fluid Science, 31, 165, 2007]. Determine the value of the average Nusselt number, Nu_D = hD/k where D = 2r_o. If the rotating disk temperature is T_s = 50°C, what is the total heat flux from the disk’s top surface for g = 1 mm, Ω = 150 rad/s? What is the total electric power requirement? What can you say about the nature of the flow between the disks?

Data From Problem 6.16

If laminar flow is induced at the surface of a disk due  to rotation about its axis, the local convection coefficient  is known to be a constant, h = C, independent of  radius. Consider conditions for which a disk of radius  r_o = 100 mm is rotating in stagnant air at T_∞ = 20°C  and a value of C = 20 W/m² · K is maintained.

If an embedded electric heater maintains a surface temperature of T_s = 50°C, what is the local heat flux at the top surface of the disk? What is the total electric power requirement? What can you say about the nature of boundary layer development on the disk?

Transcribed Image Text:

Nu, = h(r)r k = -0.456 Re 70(1+e-140G) Re 0.478