Suppose there is a test, x, that yields the distribution of test outcomes for good drugs and bad drugs shown in Figure 12.10. The bad drug curve b(x) is defined as

while the good drug curve g(x) is defined as follows: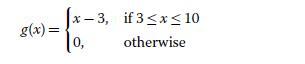

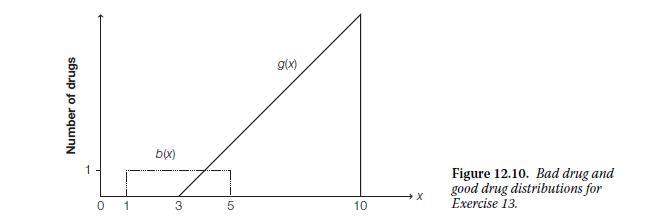
a. Let x* be the drug acceptance threshold. Let “total Type I loss” equal the total area under the bad-drug curve to the right of x*. It captures the number of bad drugs approved with this drug acceptance threshold. Write down an equation for total Type I loss as a function x∗. The function L₁(x*) should indicate how much total Type I loss there is for any value of x*.

b. Now write down a function for total Type II loss as a function of x*. This function L₂(x*) should give the number of good drugs not approved given threshold x*.

c. A loss function specifies the welfare loss caused by Type I and Type II error. If we assume society values each loss type equally, the social loss function will be the sum of the Type I loss and Type II loss. Calculate social loss as a function of x*.

d. Draw a graph of your loss function plotted against x.Minimize your function from the previous exercise to show that the optimal value of x* is 4.

e. Explain why the optimal value will always come at the intersection of the bad drug and good drug distributions if they are both continuous and overlapping.

f. Now assume that you are an FDA regulator and that, for political reasons, you regard Type I error to be twice as harmful as Type II error. Rewrite your loss function to reflect these preferences and find the FDA optimal value for x*.

g. How much total welfare loss is induced if the FDA picks its optimal threshold instead of society’s optimal threshold? Calculate your answer using society’s loss function, not the FDA’s.

Transcribed Image Text:

b(x) = 1, if 1