Consider the diffusion of urea in an agar gel discussed in Example 1.26. In this case the gel, containing a uniform initial urea concentration of \(50 \mathrm{~g} / \mathrm{L}\), is molded in the form of a \(3-\mathrm{cm}\) diameter sphere. All the sphere surface is exposed to a running supply of fresh water into which the urea diffuses. The temperature is \(278 \mathrm{~K}\) and the resistance to diffusion is assumed to reside wholly within the gel. The diffusivity of urea in this gel at this temperature was found in Example 1.26 to be \(4.7 \times 10^{-6} \mathrm{~cm}^{2} / \mathrm{s}\). How long will it take for the average urea concentration in the gel to be \(30 \mathrm{~g} / \mathrm{L}\) ?
From Crank (1975), for spherical geometry:

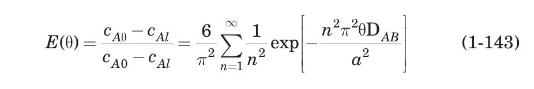
Here, \(a\) is the radius of the sphere. This series converges rapidly, and the first three terms are enough to give accurate results.

Data From Example 1.26:-

An agar gel containing a uniform urea concentration of 50 g/L is molded in the form of a 3-cm cube. Two opposite faces of the cube are exposed to a running supply of fresh water unto which urea diffuses. The other faces are protected by the mold. The temperature is 280 K. It was observed that at the end of 16.6 h the average urea concentration in the gel had fallen to 30 g/L. The resistance to diffusion may be considered as residing wholly within the gel.

(a) Calculate the diffusivity of urea in the gel at this temperature.

(b) Plot the urea concentration in the gel as a function of position on the slab currently.

(c) How long would it take for the average concentration to fall to 10 g/L?

Transcribed Image Text:

E(0)= == CAD-CAL 6 CAO CAI = T 2 1 n0D AB exp (1-143) a