Consider the square channel shown in the sketch operating under steady-state conditions. The inner surface of the channel is at a uniform temperature of \(600 \mathrm{~K}\), while the outer surface is exposed to convection with a fluid at \(300 \mathrm{~K}\) and a convection coefficient of \(50 \mathrm{~W} / \mathrm{m}^{2} \cdot \mathrm{K}\). From a symmetrical element of the channel, a twodimensional grid has been constructed and the nodes labeled. The temperatures for nodes 1, 3, 6, 8, and 9 are identified.

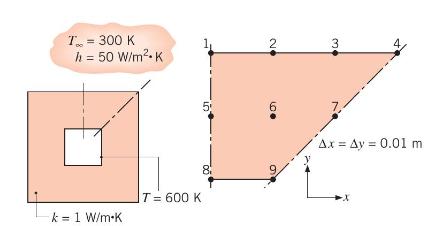
\[\begin{array}{ll}T_{1}=430 \mathrm{~K} & T_{8}=T_{9}=600 \mathrm{~K} \\T_{3}=394 \mathrm{~K} & T_{6}=492 \mathrm{~K}\end{array}\]

(a) Beginning with properly defined control volumes, derive the finite-difference equations for nodes 2,4 , and 7 and determine the temperatures \(T_{2}, T_{4}\), and \(T_{7}(\mathrm{~K})\).

(b) Calculate the rate of heat loss per unit length from the channel.

Transcribed Image Text:

T=300 K h = 50 W/m K k = 1 W/m-K T = 600 K 8 5 2 No 3 6 Ax Ay 0.01 m