Equation (2-76) can also be used for calculations of transpiration cooling, a method of cooling porous surfaces
Question:
Equation (2-76) can also be used for calculations of transpiration cooling, a method of cooling porous surfaces which are exposed to extremely hot gases by forcing a cold gas or evaporating liquid through the surface into the gas stream. Consider the following application of transpiration cooling. Air at \(900 \mathrm{~K}\) and \(1 \mathrm{~atm}\) flows past a flat, porous surface. Saturated steam at \(125 \mathrm{kPa}\) flows through the surface into the airstream to keep the surface temperature at \(523 \mathrm{~K}\). The air velocity is such that the heat-transfer coefficient would be \(1.1 \mathrm{~kW} / \mathrm{m}^{2} \cdot \mathrm{s}\) if no steam were used. From \(523 \mathrm{~K}\) to \(900 \mathrm{~K}, C_{p, A}=2.09 \mathrm{~kJ} / \mathrm{kg} \cdot \mathrm{K}\).
(a) What rate of steam flow is required?
(b) Repeat if, instead of steam, liquid water at \(298 \mathrm{~K}\) is forced through the porous surface.
Data From Equation 2-76:-
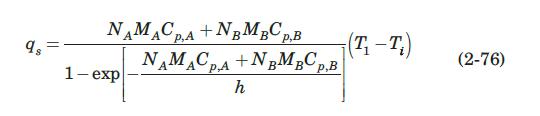
Step by Step Answer:






