For a small heat source attached to a large substrate, the spreading resistance associated with multidimensional conduction in the substrate may be approximated by the expression [Yovanovich, M. M., and V. W. Antonetti, in Adv. Thermal Modeling Elec. Comp. and Systems, Vol. 1, A. Bar-Cohen and A. D. Kraus, Eds., Hemisphere, NY, 79-128, 1988]

\(R_{t(\mathrm{sp})}=\frac{1-1.410 A_{r}+0.344 A_{r}^{3}+0.043 A_{r}^{5}+0.034 A_{r}^{7}}{4 k_{\text {sub }} A_{s, h}^{1 / 2}}\)

where \(A_{r}=A_{s, h} / A_{s, \text { sub }}\) is the ratio of the heat source area to the substrate area. Consider application of the expression to an in-line array of square chips of width \(L_{h}=5 \mathrm{~mm}\) on a side and pitch \(S_{h}=8 \mathrm{~mm}\). The interface between the chips and a large substrate of thermal conductivity \(k_{\text {sub }}=80 \mathrm{~W} / \mathrm{m} \cdot \mathrm{K}\) is characterized by a thermal contact resistance of \(R_{t, c}^{\prime \prime}=0.5 \times 10^{-4} \mathrm{~m}^{2} \cdot \mathrm{K} / \mathrm{W}\).

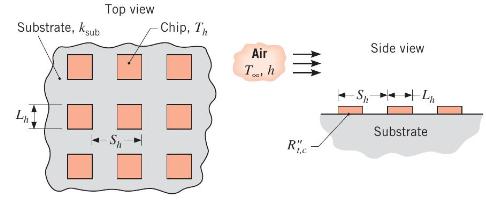
If a convection heat transfer coefficient of \(h=100\) \(\mathrm{W} / \mathrm{m}^{2} \cdot \mathrm{K}\) is associated with airflow \(\left(T_{\infty}=15^{\circ} \mathrm{C}\right)\) over the chips and substrate, what is the maximum allowable chip power dissipation if the chip temperature is not to exceed \(T_{h}=85^{\circ} \mathrm{C}\) ?

Transcribed Image Text:

Substrate, kub L Top view Chip, Th Side view Air Th R L Substrate