Pure, solid silicon is produced from a melt, as, for example, in Problem 1.37. Solid silicon is semitransparent, and the spectral absorption coefficient distribution for pure silicon may be approximated as

\[\begin{array}{ll}\kappa_{\lambda, 1}=10^{8} \mathrm{~m}^{-1} & \lambda \leq 0.4 \mu \mathrm{m} \\\kappa_{\lambda, 2}=0 \mathrm{~m}^{-1} & 0.4 \mu \mathrm{m}

(a) Determine the total absorption coefficient defined as

\[\kappa=\frac{\int_{0}^{\infty} \kappa_{\lambda} G_{\lambda}(\lambda) d \lambda}{G}\]

for irradiation from surroundings at a temperature equal to the melting point of silicon.

(b) Estimate the total transmissivity, total absorptivity, and total emissivity of an \(L=140-\mu \mathrm{m}\)-thick sheet of solid silicon at its melting point.

Data From Problem 1.37:-

One method for growing thin silicon sheets for photovoltaic solar panels is to pass two thin strings of high melting temperature material upward through a bath of molten silicon. The silicon solidifies on the strings near the surface of the molten pool, and the solid silicon sheet is pulled slowly upward out of the pool. The silicon is replenished by supplying the molten pool with solid silicon powder. Consider a silicon sheet that is \(W_{\mathrm{si}}=75 \mathrm{~mm}\) wide and \(t_{\mathrm{si}}=140 \mu \mathrm{m}\) thick that is pulled at a velocity of \(V_{\mathrm{si}}=18 \mathrm{~mm} / \mathrm{min}\). The silicon is melted by supplying electric power to the cylindrical growth chamber of height \(H=400 \mathrm{~mm}\) and diameter \(D=350\) \(\mathrm{mm}\). The exposed surfaces of the growth chamber are at \(T_{s}=350 \mathrm{~K}\), the corresponding convection coefficient at the exposed surface is \(h=8 \mathrm{~W} / \mathrm{m}^{2} \cdot \mathrm{K}\), and the surface is characterized by an emissivity of \(\varepsilon_{s}=0.9\). The solid silicon powder is at \(T_{\mathrm{s}, i}=298 \mathrm{~K}\), and the solid silicon sheet exits the chamber at \(T_{\mathrm{si}, o}=420 \mathrm{~K}\). Both the surroundings and ambient temperatures are \(T_{\infty}=T_{\text {sur }}=298 \mathrm{~K}\).

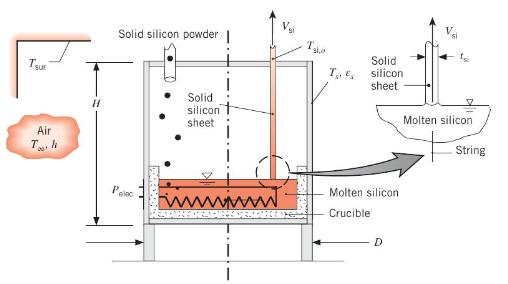
(a) Determine the electric power, \(P_{\text {elec }}\), needed to operate the system at steady state.
(b) If the photovoltaic panel absorbs a time-averaged solar flux of \(q_{\text {sol }}^{\prime \prime}=180 \mathrm{~W} / \mathrm{m}^{2}\) and the panel has a conversion efficiency (the ratio of solar power absorbed to electric power produced) of \(\eta=0.20\), how long must the solar panel be operated to produce enough electric energy to offset the electric energy that was consumed in its manufacture?

Transcribed Image Text:

Tsur Air T- Solid silicon powder Solid silicon sheet Tha I Solid TE silicon sheet Molten silicon Crucible D Molten silicon String