Repeat Problem 5.22 using \(50-\mathrm{mm}\) ceramic Pall rings as packing material. Compare your results to those of Problem 5.22.

Data From Problem 5.22:-

A tower packed with metal Montz B2-300 structured packing is to be designed to absorb \(\mathrm{SO}_{2}\) from air by scrubbing with water. The entering gas, at an \(\mathrm{SO}_{2}\)-free flow rate of \(37.44 \mathrm{~mol} / \mathrm{m}^{2}\)-s of bed cross-sectional area, contains \(20 \mathrm{~mol} \%\) of \(\mathrm{SO}_{2}\). Pure water enters at a flow rate of \(1976 \mathrm{~mol} / \mathrm{m}^{2}\)-s of bed cross-sectional area. The exiting gas is to contain only \(0.5 \mathrm{~mol} \% \mathrm{SO}_{2}\). Assume that neither air nor water will transfer between the phases and that the tower operates isothermally at \(2 \mathrm{~atm}\) and \(303 \mathrm{~K}\). Equilibrium data for solubility of \(\mathrm{SO}_{2}\) in water at \(303 \mathrm{~K}\) and \(1 \mathrm{~atm}\) have been fitted by least-squares to the equation (Seader and Henley, 1998):

(a) Derive the following operating line equation for the absorber:

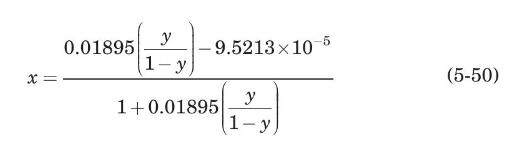
(b) If the absorber is to process \(1.0 \mathrm{~m}^{3} / \mathrm{s}\) (at \(2 \mathrm{~atm}\) and \(303 \mathrm{~K}\) ) of the entering gas, calculate the water flow rate, the tower diameter, and the gas-pressure drop per unit of packing height at the bottom of the absorber.

(c) Calculate \(N_{t G}, H_{t G}\), and the height of packing required.

Data:

Liquid:-

Density \(=998 \mathrm{~kg} / \mathrm{m}^{3} \quad\) Viscosity \(=0.7 \mathrm{cP}\)
Diffusivity \(=1.61 \times 10^{-5} \mathrm{~cm}^{2} / \mathrm{s}\)

Gas: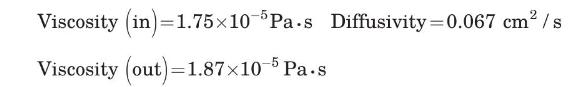

Packing characteristics are given in Problem 5.20.

Transcribed Image Text:

y = 12.697x+3148x-4.724105x3 +3.001107x-6.52410 x (5-49)