Sheet steel emerging from the hot roll section of a steel mill has a temperature of \(1000 \mathrm{~K}\), a thickness of \(\delta=2.5 \mathrm{~mm}\), and the following distribution for the spectral, hemispherical emissivity.

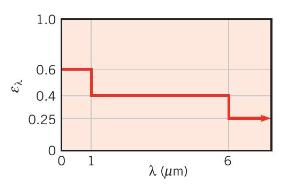
The density and specific heat of the steel are \(7900 \mathrm{~kg} / \mathrm{m}^{3}\) and \(640 \mathrm{~J} / \mathrm{kg} \cdot \mathrm{K}\), respectively. What is the total, hemispherical emissivity? Accounting for emission from both sides of the sheet and neglecting conduction, convection, and radiation from the surroundings, determine the initial time rate of change of the sheet temperature \((d T / d t)_{i}\). As the steel cools, it oxidizes and its total, hemispherical emissivity increases. If this increase may be correlated by an expression of the form \(\varepsilon=\varepsilon_{1000}[1000 \mathrm{~K} / T(\mathrm{~K})]\), how long will it take for the steel to cool from 1000 to \(500 \mathrm{~K}\) ?

Transcribed Image Text:

1.0. 0.6 0.4 0.25 0 0 1 6 (um)