The Bohart-Adams model is an exact analytic solution for fixed-bed adsorbers when the adsorption isotherm is irreversible, \(q=q_{m}\) (see Figure 9.5). The sorbate concentration in the solution is given by

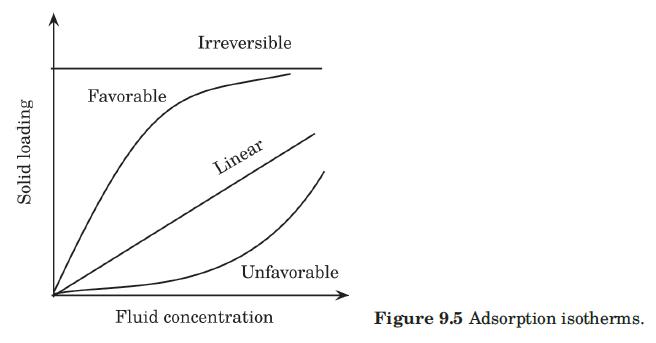
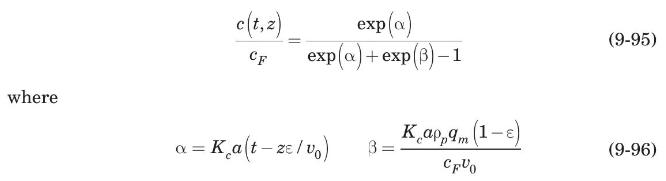
The Bohart-Adams model is commonly, but mistakenly, referred to as the Thomas model in the environmental sorption literature (Chu, 2010). Consider a fixed-bed adsorber with a total depth of \(10 \mathrm{~cm}\), a porosity of \(40 \%\), and a bulk density of \(1.5 \mathrm{~g} /\) \(\mathrm{cm}^{3}\). A dilute solution flows through the bed at a superficial velocity of \(0.8 \mathrm{~cm} / \mathrm{s}\) with a feed sorbate concentration of \(0.05 \mathrm{mg} / \mathrm{cm}^{3}\). For these conditions, \(K_{c} a=5 \times 10^{-4} \mathrm{~s}^{-1}\). The adsorption isotherm is of the Langmuir type with \(q_{m}=100 \mathrm{mg} / \mathrm{g}\) and \(K=50 \mathrm{~cm}^{3}\) / \(\mathrm{mg}\). Approximate the breakthrough curve using the Bohart-Adams model and compare it to the actual curve generated using the Thomas equation.

Data From Figure 9.5:-

Transcribed Image Text:

c(t,z) CF = exp(a) exp(a)+ exp(3)-1 (9-95) where x= Ka(t-ze/vo) B Kappam (1-e) (9-96) CFVO