3 Thomas Magnus, a private investigator, has been contacted by a potential client in Kamalo, Molokai. The call came just in time because Magnus is down to his last $10. Employment, how- ever, is conditional on Magnus's meeting the client at Kamalo within eight hours. Magnus, presently at the Masters' residence in Kipahulu, Maui, has three altemative ways to get to Kamalo. Magnus may

a. Drive to the native village of Honokahua and take an outrigger to Kamalo.

b. Drive to Honokahua and swim the 10 miles across Pailolo Channel to Kamalo.

c. Drive to Hana and ask his friend T. C. to fly him by helicopter to Kamalo.

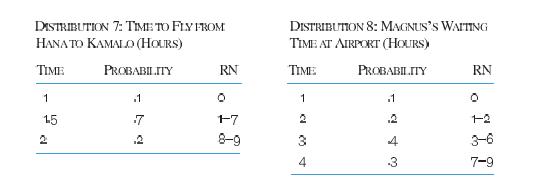
If option a is chosen, driving times to Honokahua are given in Distribution I. Once at Honokahua, Magnus must negotiate with the friendly Tai natives. Negotiations always include a few Mai Tais, so if Magnus begins to negotiate, swimming becomes impossible. Negotiations center on how much each of the three outrigger crew members will be paid. Negotiation time, crew pay, and outrigger travel time are in Distributions 3, 4, and 5, respectively. You may assume each crew member is paid the same amount. If cnew pay totals more than $10, Magnus is out of luck-trip time may then be taken to be infinity. If option b is chosen, driving times to Honokahua and swimming times are given in Distributions 1 and 6. If option c is chosen, driving times to Hana are given in Distribution 2. T. C., however, is at the airport only 10 percent of the time. If T. C. is not at the airport, Magnus will wait for him to arrive. Magnus's waiting time is given by Distribution 8. T. C. may refuse to fly for the $10 Magnus has available; Magnus puts the probability of T. C. refusing to fly for $10 at 30 percent. You may assume negotiation time is zero. If T. C. refuses, Magnus will drive to Honokahua via Kipahulu and swim to Kamalo. Helicopter flying times are given in Distribution 7. Simulate each of the three alterative transportation plans twice and, based on your simula- tion results, calculate the average trip time for each plan. Use the following random numbers in the order they appear; do not skip any random numbers.

RN: 7, 3, 0, 4, 0, 5, 3, 5, 6, 1, 6, 6, 4, 8, 4, 9, 0, 7, 7, 1, 7, 0, 6, 8, 8, 7, 9, 0, 1, 2, 9, 7, 3, 2, 3, 8, 6, 0, 6, 0, 5, 9, 7, 9, 6, 4, 7, 2, 8, 7, 8, 1, 7, 0, 5

Transcribed Image Text:

Molokai Kamalo Pailolo Channel Honokahua Maui Hana Kipahulu