Consider the vertical differentiation model presented in Section 5.3. Suppose that the quality of the product can be described by some number s_i∈ [s, sÌ…] ⊂ R+. Consumers are identified by θ ∈ [θ, θ] ⊂ R₊, which measures their preference for quality. Consumers are distributed uniformly on [θ, θ] and are of mass

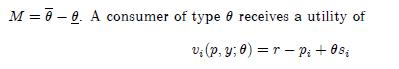when consuming a unit of good i (where γ is supposed to be sufficiently large, so that all consumers buy in the market). Two firms compete in the market. We look for the sub-game-perfect equilibria of the following two-stage game: firms first choose the quality of their product and then compete in prices. Contrary to what was assumed in Section 5.3, we assume now that the marginal cost of production depends on quality. We denote by C (q_i, s_i) the cost of firm i producing q_i units at a quality s_i and we assume

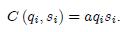With a > 0, this formulation introduces a trade-off between quality and quantity as the marginal cost of production, as_i, increases with quality. That is, if the firm increases one dimension (quality or quantity), the cost of providing the other dimension increases and the amount of this other dimension is thus reduced. An example of such an inverse relationship between quality and quantity  can be found in the way an instructor teaches a course: as the number of students enrolled (i.e., quantity) increases, the cost for the instructor of providing  a high-quality teaching increases (given the time available, the instructor’s ability to meet students outside of class, or to provide students with feedback on their assignments, inevitably decreases with the number of students enrolled). To guarantee interior solutions in the pricing game, we assume

1. Consider the second stage of the game where firms set prices simultaneously, taking the qualities as given. Firm 1 produces quality s₁ and firm 2 produces quality s₂, with the convention that s₁ < s₂. Derive the Nash equilibrium in prices and express the equilibrium quantities and profits of the two firms at stage 2.

2. Consider now the first stage of the game where firms simultaneously choose the quality of their product.

(a) Show that (s₁, s₂) = (s, sÌ…) or (sÌ…, s) are the equilibrium quality choices of the game.

(b) What is the effect of a stronger quality-quantity trade-off (i.e., of a larger value of parameter a)? Discuss.

Transcribed Image Text:

M = 6 – 0. A consumer of type 0 receives a utility of v: (p, y; 0) = r – Pi + Os; C (qi, Si) = aqiSi.