Equilibrium uniqueness in the Cournot model

Consider an oligopoly with n firms that produce homogeneous goods and compete à la Cournot. Inverse demand is given by P (Q) with P? (Q) i (q_i) with C²_i (q_i) > 0 and C² (q_i) ? 0. Denote q-i = ?_{j ? I} q_j.

1. Compute the first- and second order condition of firm i. Under which conditions is the profit function of firm i, ?_i, strictly concave?

2. Compute the slope of the best-reply function of firm i, dqi /dq - i. In which interval is this slope? A sufficient condition for uniqueness of a Cournot equilibrium is (see, e.g., Tirole (1999), page 226)

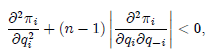
3. Suppose that demand is concave and that marginal costs are constant. For which number of n is the condition above satisfied?

4. Suppose that

Is there a unique equilibrium for any n?