Consider a dividend-paying asset priced as

\[S_{t}=S_{0} \mathrm{e}^{(r-\delta) t+\sigma \widehat{B}_{t}-\sigma^{2} t / 2}, \quad t \geqslant 0\]

where \(r>0\) is the risk-free interest rate, \(\delta \geqslant 0\) is a continuous dividend rate, \(\left(\widehat{B}_{t}\right)_{t \in \mathbb{R}_{+}}\)is a standard Brownian motion under the risk-neutral probability measure \(\mathbb{P}^{*}\), and \(\sigma>0\) is the volatility coefficient. Consider the American put option with payoff

\[\left(\kappa-S_{\tau}\right)^{+}= \begin{cases}\kappa-S_{\tau} & \text { if } S_{\tau} \leqslant \kappa \\ 0 & \text { if } S_{\tau}>\kappa\end{cases}\]

when exercised at the stopping time \(\tau>0\). Given \(L \in(0, \kappa)\) a fixed level, consider the following exercise strategy for the above option:

- If \(S_{t} \leqslant L\), then exercise at time \(t\).

- If \(S_{t}>L\), wait until the hitting time \(\tau_{L}:=\inf \left\{u \geqslant t: S_{u}=L\right\}\), and exercise the option at time \(\tau_{L}\).

a) Give the intrinsic option value at time \(t=0\) in case \(S_{0} \leqslant L\).

In what follows we work with \(S_{0}=x>L\).

b) Show that for all \(\lambda \in \mathbb{R}\) the process \(\left(Z_{t}^{(\lambda)}\right)_{t \in \mathbb{R}_{+}}\)defined as

\[Z_{t}^{(\lambda)}:=\left(\frac{S_{t}}{S_{0}}\right)^{\lambda} \mathrm{e}^{-\left((r-\delta) \lambda-\lambda(1-\lambda) \sigma^{2} / 2\right) t}\]
is a martingale under the risk-neutral probability measure \(\mathbb{P}^{*}\).

c) Show that \(\left(Z_{t}^{(\lambda)}\right)_{t \in \mathbb{R}_{+}}\)can be rewritten as \[Z_{t}^{(\lambda)}=\left(\frac{S_{t}}{S_{0}}\right)^{\lambda} \mathrm{e}^{-r t}, \quad t \geqslant 0\]
for two values \(\lambda_{-} \leqslant 0 \leqslant \lambda_{+}\)of \(\lambda\) that can be computed explicitly.

d) Choosing the negative solution \(\lambda_{-}\), show that \[0 \leqslant Z_{t}^{\left(\lambda_{-}\right)} \leqslant\left(\frac{L}{S_{0}}\right)^{\lambda_{-}}, \quad 0 \leqslant t \leqslant \tau_{L}\]

e) Let \(\tau_{L}\) denote the hitting time \[\tau_{L}=\inf \left\{u \in \mathbb{R}_{+}: S_{u} \leqslant L\right\}\]
By application of the Stopping Time Theorem 14.7 to the martingale \(\left(Z_{t}\right)_{t \in \mathbb{R}_{+}}\), show that \[\begin{equation*}
\mathbb{E}^{*}\left[\mathrm{e}^{-r \tau_{L}}\right]=\left(\frac{S_{0}}{L}\right)^{\lambda_{-}}, \tag{15.33}
\end{equation*}\]
with \[\begin{equation*}
\lambda_{-}:=\frac{-\left(r-\delta-\sigma^{2} / 2\right)-\sqrt{\left(r-\delta-\sigma^{2} / 2\right)^{2}+4 r \sigma^{2} / 2}}{\sigma^{2}} . \tag{15.34}
\end{equation*}\]

f) Show that for all \(L \in(0, K)\) we have \[\begin{aligned}
\mathbb{E}^{*} & {\left[\mathrm{e}^{-r \tau_{L}}\left(K-S_{\tau_{L}}\right)^{+} \mid S_{0}=x\right] } \\
& = \begin{cases}K-x, & 0(K-L)\left(\frac{x}{L}\right)^{\frac{-\left(r-\delta-\sigma^{2} / 2\right)-\sqrt{\left(r-\delta-\sigma^{2} / 2\right)^{2}+4 r \sigma^{2} / 2}}{\sigma^{2}}}, & x \geqslant L .\end{cases}
\end{aligned}\]
g) Show that the value \(L^{*}\) of \(L\) that maximizes \[f_{L}(x):=\mathbb{E}^{*}\left[\mathrm{e}^{-r \tau_{L}}\left(K-S_{\tau_{L}}\right)^{+} \mid S_{0}=x\right]\]
for every \(x>0\) is given by \[L^{*}=\frac{\lambda_{-}}{\lambda_{-}-1} K\]
h) Show that \[f_{L^{*}}(x)= \begin{cases}K-x, & 0)^{\lambda_{-}-1}\left(\frac{x}{-\lambda_{-}}\right)^{\lambda_{-}}, & x \geqslant L^{*}=\frac{\lambda_{-}}{\lambda_{-}-1} K\end{cases}\]
i) Show by hand computation that \(f_{L^{*}}(x)\) satisfies the variational differential equation

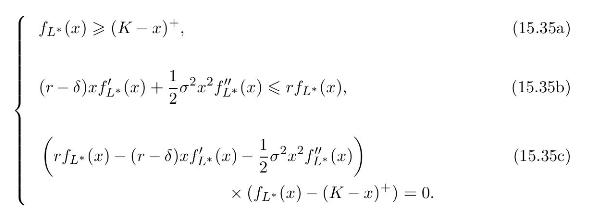
j) Using Itô's formula, check that the discounted portfolio value process \[t \mapsto \mathrm{e}^{-r t} f_{L^{*}}\left(S_{t}\right)\]
is a supermartingale.
k) Show that we have \[f_{L^{*}}\left(S_{0}\right) \geqslant \operatorname{Sup}_{\tau \text { Stopping time }} \mathbb{E}^{*}\left[\mathrm{e}^{-r \tau}\left(K-S_{\tau}\right)^{+} \mid S_{0}\right] .\]
l) Show that the stopped process \[s \mapsto \mathrm{e}^{-\left(s \wedge \tau_{L^{*}}\right) r} f_{L^{*}}\left(S_{s \wedge \tau_{L^{*}}}\right), \quad s \geqslant 0,\]
is a martingale, and that \[f_{L^{*}}\left(S_{0}\right) \leqslant \operatorname{Sup}_{\tau \text { Stopping time }} \mathbb{E}^{*}\left[\mathrm{e}^{-r \tau}\left(K-S_{\tau}\right)^{+}\right] .\]

m) Fix \(t \in \mathbb{R}_{+}\)and let \(\tau_{L^{*}}\) denote the hitting time \[\tau_{L^{*}}=\inf \left\{u \geqslant t: S_{u}=L^{*}\right\}\]
Conclude that the price of the perpetual American put option with dividend is given for all \(t \in \mathbb{R}_{+}\)by \[\begin{aligned}
f_{L^{*}}\left(S_{t}\right) & =\mathbb{E}^{*}\left[\mathrm{e}^{-\left(\tau_{\left.L^{*}-t\right) r}\left(K-S_{\tau_{L^{*}}}\right)^{+} \mid S_{t}\right]}\right. \\
& = \begin{cases}K-S_{t}, & 0\left(\frac{1-\lambda_{-}}{K}\right)^{\lambda_{-}-1}\left(\frac{S_{t}}{-\lambda_{-}}\right)^{\lambda_{-}}, & S_{t} \geqslant \frac{\lambda_{-}}{\lambda_{-}-1} K\end{cases}
\end{aligned}\]
where \(\lambda_{-}\} .\]

m) Fix \(t \in \mathbb{R}_{+}\)and let \(\tau_{L^{*}}\) denote the hitting time \[\tau_{L^{*}}=\inf \left\{u \geqslant t: S_{u}=L^{*}\right\}\]
Conclude that the price of the perpetual American put option with dividend is given for all \(t \in \mathbb{R}_{+}\)by \[\begin{aligned}
f_{L^{*}}\left(S_{t}\right) & =\mathbb{E}^{*}\left[\mathrm{e}^{-\left(\tau_{\left.L^{*}-t\right) r}\left(K-S_{\tau_{L^{*}}}\right)^{+} \mid S_{t}\right]}\right. \\
& = \begin{cases}K-S_{t}, & 0\left(\frac{1-\lambda_{-}}{K}\right)^{\lambda_{-}-1}\left(\frac{S_{t}}{-\lambda_{-}}\right)^{\lambda_{-}}, & S_{t} \geqslant \frac{\lambda_{-}}{\lambda_{-}-1} K\end{cases}
\end{aligned}\]
where \(\lambda_{-}\} .\]

Transcribed Image Text:

f(x)(K), (r 6)x- (x) + ox " + (x)