In a market model with two time instants (t=0) and (t=1) and risk-free interest rate (r), consider

Question:

In a market model with two time instants $t=0$ and $t=1$ and risk-free interest rate $r$, consider

- a riskless asset valued $S_{0}^{(0)}$ at time $t=0$, and value $S_{1}^{(0)}=(1+r) S_{0}^{(0)}$ at time $t=1$.

- a risky asset with price $S_{0}^{(1)}$ at time $t=0$, and three possible values at time $t=1$, with \(a

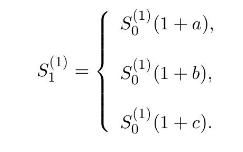
image text in transcribed

a) Show that this market is without arbitrage but not complete.

b) In general, is it possible to hedge (or replicate) a claim with three distinct claim payoff values $C_{a}, C_{b}$, and $C_{c}$ in this market?

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Introduction To Stochastic Finance With Market Examples

ISBN: 9781032288277

2nd Edition

Authors: Nicolas Privault

See More Books

Question Posted: Feb 25, 2024 08:00 AM

See More Questions

13. What is a lower bound for the price of 3-month call option on a non- dividend-paying stock when the stock price is $50, the strike price is $45, and the 3-month risk-free interest rate is 8%?...
Consider a one-step market model with two time instants $t=0$ and $t=1$ and two assets: - a riskless asset $\pi$ with price $\pi_{0}$ at time $t=0$ and value $\pi_{1}=\pi_{0}(1+r)$ at...
do the following,..... Write program that reads a person's first and last names, separated by a space. Then the program outputs last name, comma, first name. Create program that takes in user input...
Add to Graph a method subgraph() that takes a SET as its argument and returns the induced subgraph (the graph comprising the specified vertices together with all edges from the original graph that...
The following bar graph represents the boiling temperature, the temperature at which a substance changes from liquid to gas at standard atmospheric pressure. Use this graph to answer below Exercises....
Summarize the elements of effective opt-in email.
Suppose $X \sim N(0,1)$ and $W_{n} \sim \chi_{n}^{2}$ independently for any positive integer $n$. Let $V_{n}=X / \sqrt{W_{n}} / n$. a. We know $V_{n} \sim t_{n}$. Show that $V_{n}^{2}$ follows an...
Brown & Co. issued seven-year bonds two years ago that can be called aft er two years. The bonds make semiannual coupon payments at a coupon rate of 7.875 percent. Each bond has a market value of...
1. Corporate Finance deals with raising funds for Private Companies, Corporate entities and Governments. What are these funds not used for ? Explain
We consider a riskless asset valued $S_{1}^{(0)}=S_{0}^{(0)}$, at times $k=0$, 1 , with risk-free interest rate is $r=0$, and a risky asset $S^{(1)}$ whose return...
a) Consider the following market model: b) Consider the following market model: c) Consider the following market model: 8(1) b a (1+r)s()
Determine whether the given set of invertible n x n matrices with real number entries is a subgroup of GL(n, R). The upper-triangular n x n matrices with no zeros on the diagonal
In the following $R$ output, some of the numbers have been accidentally erased. Recompute them, using the numbers still available. There are $n=20$ points in the data set. Coefficients:...
The National Center for Health Statistics interviewed 5409 adult smokers in 2015 , and 2636 of them said they had tried to quit smoking during the past year. Consider this to be a random sample. a....
The concentration of carbon monoxide (CO) in a gas sample is measured by a spectrophotometer and found to be $85 \mathrm{ppm}$. Through long experience with this instrument, it is believed that its...
Refer to Exercise 18. a. Find a 95 % 95 % upper confidence bound for the mean time. b. Find a 98 % 98 % lower confidence bound for the mean time. Data From Exercise 18: One step in the manufacture of...
Refer to Exercise 32. For each duration, the confidence interval at 40 % 40 % humidity is narrower than the one at 75 % 75 % humidity. Which of the following is the best explanation for this? i....
A room contains air in which the speed of sound is 343 m/s. The walls of the room are made of concrete, in which the speed of sound is 1 850 m/s. (a) Find the critical angle for total internal...
If |62x|>9, which of the following is a possible value of x? A. 2 B. 1 C. 0 D. 4 E. 7
Assume that banks must hold a 2 percent reserve percentage against transaction account balances up to and including $40 million. For transaction accounts above $40 million, the required reserve...
Assume that the Fed decides to increase the required reserve percentage on transaction accounts above $40 million from 8 percent to 10 percent. All other information remains the same as given in...
Identify the seven individuals who served as chairs of the Fed Board of Governors since the early 1950s. Indicate each individuals approximate time and length of service as chair.
The common stock of Flavorful Teas has an expected return of 20.4 percent. The return on the market is 14 percent and the risk-free rate of return is 3.6 percent. Calculate the beta of this stock.
What are the key principles underlying enzyme catalysis, and how do enzyme structures contribute to their remarkable specificity and efficiency in biochemical reactions ?
Define, measure, analyze, improve, and control (DMAIC) is used when implementing Lean Six Sigma in what processes?

In a market model with two time instants (t=0) and (t=1) and risk-free interest rate (r), consider

Question:

S() s() (1 + a), s() (1+b), S()(1 + c).

Step by Step Answer:

a We need to search for po...View the full answer

Introduction To Stochastic Finance With Market Examples

Students also viewed these Business questions