Use the tabular method discussed in Section 8.4.1 to find a minimum cost SOP realization for the function

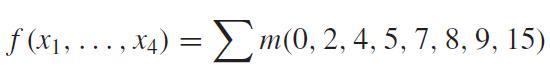
Data From Section 8.4.1

A Tabular Method for Minimization
A tabular approach for minimization was proposed in the 1950s by Willard Quine [5] and Edward McCluskey [6]. It became popular under the name Quine-McCluskey method.
While it is not efficient enough to be used in modern CAD tools, it is a simple method that illustrates the key issues. We will present it using the cubical notation discussed in Section 8.3.

Generation of Prime Implicants

As mentioned in Section 8.3, the prime implicants of a given logic function f are the largest possible k-cubes for which f = 1. For incompletely specified functions, which include a set of don’t-care vertices, the prime implicants are the largest k-cubes for which either f = 1 or f is unspecified.

Assume that the initial specification of f is given in terms of minterms for which f = 1.

Also, let the don’t-cares be specified as minterms. This allows us to create a list of vertices for which either f = 1 or it is a don’t-care condition. We can compare these vertices in pairwise fashion to see if they can be combined into larger cubes. Then we can attempt to combine these new cubes into still larger cubes and continue the process until we find the prime implicants.

f (x, ..., x4) = m(0, 2, 4, 5, 7, 8, 9, 15)