A weight W is supported by two cables anchored a distance D apart (see Figure P35). The cable length L_AB is given, but the length L_AC is to be selected. Each cable can support a maximum tension force equal to W.

Figure P35.

 

For the weight to remain stationary, the total horizontal force and total vertical force must each be zero. This principle gives the equations

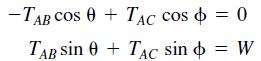
We can solve these equations for the tension forces T_AB and T_AC if we know the angles θ and ϕ. From the law of cosines

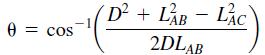
From the law of sines

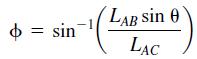
For the given values D = 6 ft, LAB = 3 ft, and W = 2000 lb, use a loop in MATLAB to find L_Acmin, the shortest length L_AC we can use without T_AB or T_AC exceeding 2000 lb. Note that the largest L_AC can be is 6.7 ft (which corresponds to 0 = 90°). Plot the tension forces T_AB and T_AC on the same graph versus LAC for L_Aanin ≤ L_AC ≤ 6.7.

D C A LAB LC B W to