An engine flywheel has an eccentricity of \(0.8 \mathrm{~cm}\) and mass \(38 \mathrm{~kg}\). Assuming a damping ratio of 0.05 , what is the necessary stiffness of the bearings to limit its whirl amplitude to \(0.8 \mathrm{~mm}\) at all speeds between 1000 and \(2000 \mathrm{rpm}\) ? Refer to Chapter Problem 4.32 for an explanation of whirling.

Data From Chapter Problem 4.32:
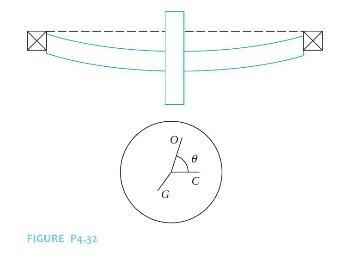
Whirling is a phenomenon that occurs in a rotating shaft when an attached rotor is unbalanced. The motion of the shaft and the eccentricity of the rotor cause an unbalanced inertia force, pulling the shaft away from its centerline, causing it to bow. Use Figure P4.32 to show that the amplitude of whirling is
\[
X=e \Lambda(r, \zeta)
\]
where \(e\) is the distance from the center of mass of the rotor to the axis of the shaft.

Transcribed Image Text:

FIGURE P4.32 C