For a single degree of freedom spring-mass-damper system with (m=0.2 mathrm{lb}_{mathrm{m}}), (k=2.5 times 10^{3} mathrm{lb}_{mathrm{f}} / mathrm{in}
Question:
For a single degree of freedom spring-mass-damper system with \(m=0.2 \mathrm{lb}_{\mathrm{m}}\), \(k=2.5 \times 10^{3} \mathrm{lb}_{\mathrm{f}} / \mathrm{in} ., c=10.92 \mathrm{lb}_{\mathrm{f}-\mathrm{s}} / \mathrm{ft}, x_{0}=0.1\) in., and \(\dot{x}_{0}=0\), complete the following for the case of free vibration.
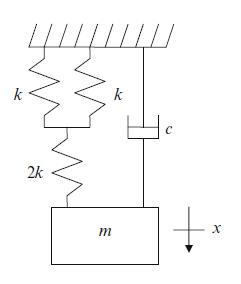
Fig. P2.5 Single degree of freedom spring-mass-damper system under free vibration
(a) Determine the equivalent spring constant (in \(\mathrm{lb}_{\mathrm{f}} / \mathrm{in}\) ) for the spring configuration shown in the figure.
(b) Determine the force (in \(\mathrm{lb}_{\mathrm{f}}\) ) required to cause the initial displacement of 0.1 in. (assume the system was at static equilibrium prior to introducing the initial displacement).
(c) Calculate the damping ratio. You will need the units correction factor: \(\left(32.2 \mathrm{ft}-1 \mathrm{~b}_{\mathrm{m}}\right) /\left(\mathrm{lb}_{\mathrm{f}}-\mathrm{s}^{2}\right)\). Is this system underdamped or overdamped?
(d) Calculate the damped natural frequency (in \(\mathrm{Hz}\) ).
Step by Step Answer:

Mechanical Vibrations Modeling And Measurement
ISBN: 119669
1st Edition
Authors: Tony L. Schmitz , K. Scott Smith





