For the single degree of freedom torsional system under harmonic forced vibration (see Fig. P3.4), complete parts a through c if \(J=40 \mathrm{~kg}-\mathrm{m}^{2} / \mathrm{rad}\), \(C=150 \mathrm{~N}-\mathrm{m}-\mathrm{s} / \mathrm{rad}, K=5 \times 10^{5} \mathrm{~N}-\mathrm{m} / \mathrm{rad}\), and \(T_{0}=65 \mathrm{~N}-\mathrm{m}\).

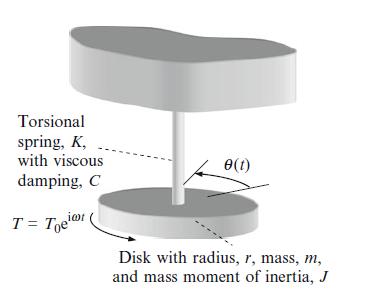
Fig. P3.4 Single degree of freedom torsional system under harmonic forced vibration

(a) Calculate the undamped natural frequency (rad/s) and damping ratio.
(b) Sketch the Argand diagram (complex plane representation) of \(\frac{\theta}{T}(\omega)\). Numerically identify key frequencies (rad/s) and amplitudes ( \(\mathrm{rad} / \mathrm{N}-\mathrm{m})\).
(c) Given a forcing frequency of \(100 \mathrm{rad} / \mathrm{s}\) for the harmonic external torque, determine the phase (in rad) between the torque and corresponding steadystate vibration of the system, \(\theta\).

Transcribed Image Text:

Torsional spring, K, with viscous damping, C T=Toe" i@t e(t) Disk with radius, r, mass, m, and mass moment of inertia, J