The center of the thin disk of Figure P3.48 is displaced a distance (delta) and the disk
Question:
The center of the thin disk of Figure P3.48 is displaced a distance \(\delta\) and the disk released. The coefficient of friction between the disk and the surface is \(\mu\). The initial displacement is sufficient to cause the disk to roll and slip.
(a) Derive the differential equation governing the motion when the disk rolls and slips.
(b) When the displacement of the mass center from equilibrium becomes small enough, the disk rolls without slip. At what displacement does this occur?
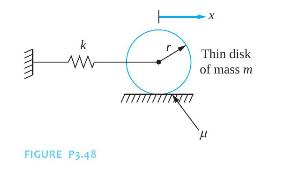
(c) Derive the differential equation governing the motion when the disk rolls without slip.
(d) What is the change in amplitude per cycle of motion?
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Answered By
Aysha Ali
my name is ayesha ali. i have done my matriculation in science topics with a+ . then i got admission in the field of computer science and technology in punjab college, lahore. i have passed my final examination of college with a+ also. after that, i got admission in the biggest university of pakistan which is university of the punjab. i am studying business and information technology in my university. i always stand first in my class. i am very brilliant client. my experts always appreciate my work. my projects are very popular in my university because i always complete my work with extreme devotion. i have a great knowledge about all major science topics. science topics always remain my favorite topics. i am also a home expert. i teach many clients at my home ranging from pre-school level to university level. my clients always show excellent result. i am expert in writing essays, reports, speeches, researches and all type of projects. i also have a vast knowledge about business, marketing, cost accounting and finance. i am also expert in making presentations on powerpoint and microsoft word. if you need any sort of help in any topic, please dont hesitate to consult with me. i will provide you the best work at a very reasonable price. i am quality oriented and i have 5 year experience in the following field.
matriculation in science topics; inter in computer science; bachelors in business and information technology
_embed src=http://www.clocklink.com/clocks/0018-orange.swf?timezone=usa_albany& width=200 height=200 wmode=transparent type=application/x-shockwave-flash_
11+ Reviews
14+ Question Solved
Related Book For 
Question Posted:
