The power P dissipated as heat in a resistor R as a function of the current i(t) passing through it is P = i²R. The energy E(t) lost as a function of time is the time integral of the power. Thus

 

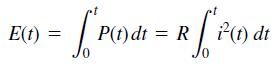
If the current is measured in amperes, the power is in watts and the energy is in joules (1 W = 1 J/s). Suppose that a current i(t) = 0.2[1 + sin(0.2t)] A is applied to the resistor.

a. Determine the energy E(t) dissipated as a function of time.

b. Determine the energy dissipated in 1 min if R = 1000 Ω.

Transcribed Image Text:

E(t) P(t)dt = R P(1) dt 0.