Let 3 contains all size 3 columns of 0s and 1s. A string of symbols in

Let

Σ₃ contains all size 3 columns of 0s and 1s. A string of symbols in Σ₃ gives three rows of 0s and 1s. Consider each row to be a binary number and let

B = {w ∈ Σ^*₃ | the bottom row of w is the sum of the top two rows}.

For example,

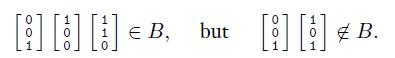
Show that B is regular. Working with BR is easier. You may assume the result claimed in Problem 1.31.

Problem 1.31.

For any string w = w₁w₂ · · ·w_n, the reverse of w, written w^R, is the string w in reverse order, w_n · · ·w₂w₁. For any language A, let A^R = {w^R| w ∈ A}. Show that if A is regular, so is A^R.

Transcribed Image Text:

Eg = {[}] • [] - [3]-