Let

 

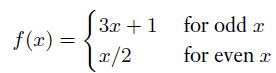
for any natural number x. If you start with an integer x and iterate f, you obtain a sequence, x, f(x), f(f(x)), . . . . Stop if you ever hit 1. For example, if x = 17, you get the sequence 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1. Extensive computer tests have shown that every starting point between 1 and a large positive integer gives a sequence that ends in 1. But the question of whether all positive starting points end up at 1 is unsolved; it is called the 3x + 1 problem. Suppose that A_TM were decidable by a TM H. Use H to describe a TM that is guaranteed to state the answer to the 3x + 1 problem.

Transcribed Image Text:

3x +1 for odd 2/2 f(x) = for even r