Alice has a copy of a long?n-bit file?A?=??a_n-1, a_n-2, . . . , a₀?, and Bob similarly has an?n-bit file?B?=??b_n-1, b_n-2, . . . , b₀?. Alice and Bob wish to know if their files are identical. To avoid transmitting all of?A?or?B, they use the following fast probabilistic check. Together, they select a prime?q > 1000n?and randomly select an integer?x?from?{0, 1, . . . , q???1}. Then, Alice evaluates

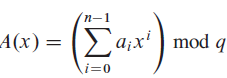
and Bob similarly evaluates B(x). Prove that if A ? B, there is at most one chance in 1000 that A(x) = B(x), whereas if the two files are the same, A(x) is necessarily the same as B(x).

Transcribed Image Text:

n-1 A(х) — Σαχ mod q aj i=0