In the?parallel-machine-scheduling problem, we are given?n?jobs,?J₁, J₂, . . . ,J_n, where each job?J_k has an associated nonnegative processing time of?p_k. We are also given?m?identical machines,?M₁, M₂, . . . ,M_m. Any job can run on any machine.

A?schedule?specifies, for each job?J_k, the machine on which it runs and the time period during which it runs. Each job?J_k must run on some machine?M_i for?pk?consecutive time units, and during that time period no other job may run on?M_i. Let?C_k denote the?completion time?of job?J_k, that is, the time at which job?J_k completes processing. Given a schedule, we define?C_max =?max1???j???n?C_j to be the?makespan?of the schedule. The goal is to find a schedule whose makespan is minimum.

For example, suppose that we have two machines?M₁ and?M₂ and that we have four jobs?J₁, J₂, J₃, J₄, with?p₁ =?2,?p₂ =?12,?p₃ =?4, and?p₄ =?5. Then one possible schedule runs, on machine?M₁, job?J₁ followed by job?J₂, and on machine?M₂, it runs job?J₄ followed by job?J₃. For this schedule,?C₁ =?2,?C₂ =?14,

C₃ =?9,?C₄ =?5, and?C_max =?14. An optimal schedule runs?J₂ on machineM₁, and it runs jobs?J₁,?J₃, and?J₄ on machine?M₂. For this schedule,?C₁ =?2,?C₂ =?12,?C₃ =?6,?C₄ =?11, and?C_max =?12.

Given a parallel-machine-scheduling problem, we let?C^*_max denote the makespan of an optimal schedule.

a.?Show that the optimal makespan is at least as large as the greatest processing time, that is,

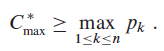
b.?Show that the optimal makespan is at least as large as the average machine load, that is,

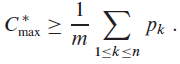
Suppose that we use the following greedy algorithm for parallel machine scheduling. whenever a machine is idle, schedule any job that has not yet been scheduled.

c.?Write pseudocode to implement this greedy algorithm. What is the running time of your algorithm?

d.?For the schedule returned by the greedy algorithm, show that

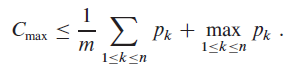
Conclude that this algorithm is a polynomial-time 2-approximation algorithm.

|C* max Pe 1