At numerous places in chemical plants there is a need for a pipe of length L to
Question:
At numerous places in chemical plants there is a need for a pipe of length L to carry a given fluid at a specified flow rate Q. An appropriate pipe diameter D must be chosen by the designer. Larger-diameter pipes are more expensive to buy and install but cheaper to operate. More precisely, the total annual cost C of a pipe can be expressed as![]()
Embedded in the dimensional constant K1 are the purchase, installation, and maintenance costs of the pipe and associated fittings, each per unit length and each put on an annual basis by assuming a certain lifetime for the system (Peters et al., 2003, pp. 401–406). For steel pipe, n ≅ 1.5. The power that a pump must deliver for flow through a straight pipe is Q|Δ℘|. The coefficient K2 is the product of the electric rate, the operating time per year, and factors that account for pump efficiency and pressure drops in fittings. The fixed costs increase with D but the pumping costs decrease, such that there is an optimal value of D.
(a) In economic calculations the friction factor can be approximated as
where a and b are constants. Peters et al. (2003) suggest a= 0.04 and b = 0.16 for turbulent flow in new steel pipes; Eqs. (2.2-6) or (2.2-9) also could be used, depending on the range of Re. Show that the diameter D* that minimizes C is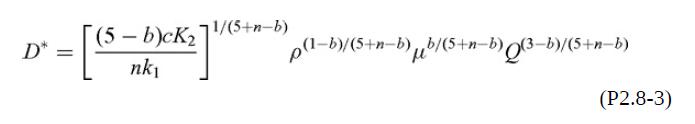
and derive an expression for the dimensionless constant c.
(b) By examining the exponents in Eq. (P2.8-3), show that there is only a weak dependence of D* on ρ and μ, for either laminar or turbulent flow. Thus, for a given Q there is one fairly narrow range of D* for low-viscosity liquids and another for gases.
(c) Let U* be the mean velocity when D = D*. Show that
for turbulent flow. Thus, unlike D*, U* is nearly independent of Q. For Schedule 40 steel pipe, U* for liquids is typically between 1.8 and 2.4 m/s (Tilton, 2007).
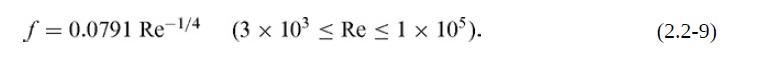
Step by Step Answer:

Introduction To Chemical Engineering Fluid Mechanics
ISBN: 9781107123779
1st Edition
Authors: William M. Deen





