Consider steady water flow in the open, rectangular channel in Fig. P2.11, which might be part of an irrigation or drainage system. The flow is due to gravity. The channel has a width W, is filled to a level H, and its sides and bottom each have a roughness height k. It is inclined at an angle θ that is small enough for the slope (tan θ) to be approximated as S = sin θ. Assuming these quantities are all known, it is desired to predict the mean velocity U.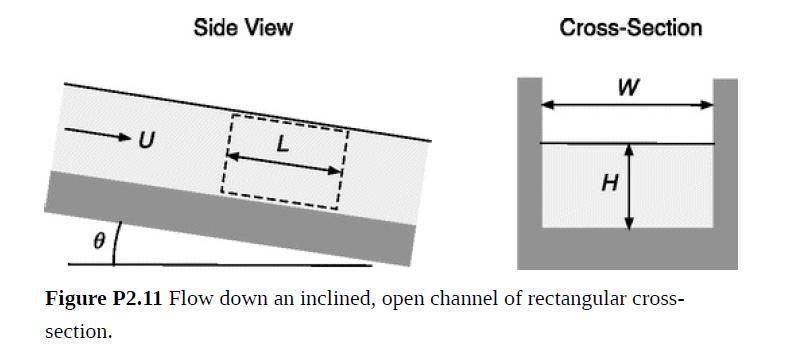

(a) What can you conclude about U from dimensional analysis? (Include U, g, and H in the principal dimensionless group.)

(b) The shear stress exerted on a liquid by an adjacent gas is typically negligible. With that in mind, use a force balance for a length L of channel (Fig. P2.11) to relate the shear stress τ_w at the solid surfaces to ρ, g, S, W, and H.

(c) If an appropriate hydraulic diameter is used, the force balance of part (b) will apply to an open channel of any shape. To permit such a generalization, how should DH be defined?

(d) In open-channel flow Re and k/DH are each typically large enough for f to be independent of Re (i.e., to be in the fully rough regime). When this is so, show that

If, as recommended by the ASCE for open-channel flow, Eq. (2.5-1) is modified to

then Eq. (P2.11-1) is nearly equivalent to the Gauckler–Manning formula (Sturm, 2010, pp. 114–123). In that widely used equation f is approximated as

Transcribed Image Text:

0 Side View L Cross-Section W H Figure P2.11 Flow down an inclined, open channel of rectangular cross- section.