Figure P12.13 shows a conical diffuser, a tube segment that tapers outward linearly in the direction of flow. Its local diameter is D(z) = D₁ + (D₂ − D₁)(z/L). The rate of diameter increase corresponds to an angle θ between the tube wall and centerline. It is desired to predict the loss coefficient K for small values of θ.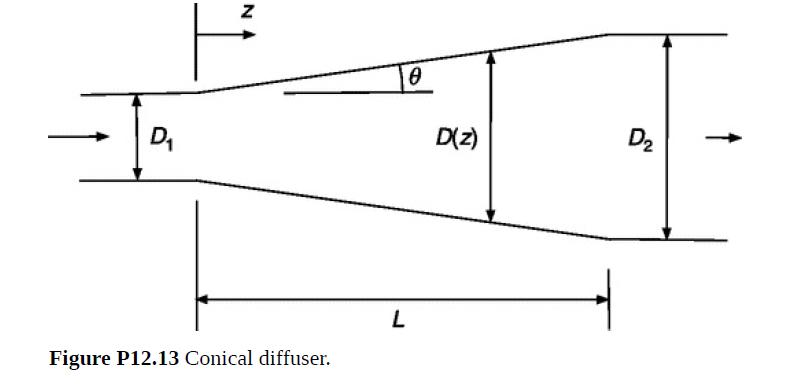

(a) For turbulent flow, show that the pressure increase in the diffuser is

where β = D₁⁄D₂.

(b) For small θ, the loss for incompressible flow can be estimated using Eq. (12.4-11). By integrating the differential loss over the length of the diffuser, show that, if the friction factor fis approximately constant, then

Notice that this reduces to the loss coefficient in a plain tube, K = 4Lf/D, for β → 1.

(c) Let

be the inlet Reynolds number. Assuming the wall is smooth and basing f on

calculate K for D₂ = 2D₁ and L = 10D₁. What percentage reduction in P₂ − P₁ is predicted to be caused by the viscous loss? How much would that be affected if f were based on

The wall angle for these dimensions, θ = tan ⁻¹(0.05) = 2.9°, is said to be within the range where the approach in part (b) is accurate (θ < 3.5°) (Tilton, 2007, pp. 6–17).

Transcribed Image Text:

- D₁ Z Figure P12.13 Conical diffuser. L 0 D(z) D₂