It is desired to estimate the entrance length L_E for laminar flow at large Re in a parallel-plate channel with wall spacing 2H and mean velocity U. In such a channel the velocity profile develops much as in Fig. P12.2. During the transition from plug flow at the inlet to the final parabolic profile, “shear layers” next to the walls accompany a “core” where the profile is flat. The shear layers are like laminar boundary layers and the core resembles an outer region. Let δ(x) and u(x) be the shear-layer thickness and core velocity, respectively.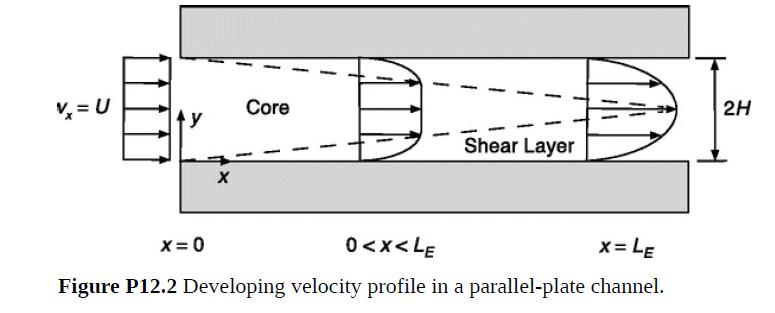

(a) As a first approximation, assume that δ(x) equals the boundary-layer thickness for flow past a flat plate. Show that, consistent with Eq. (12.2-1) for Re ≫ 1, this gives a relationship of the form

where a is a constant and

(b) Using the integral analysis in Example 9.4-1, show that a ranges from 0.017 to 0.042, depending on whether velocity profile (1), (2), or (3) of Table 9.2 is used.

(c) Whereas for a flat plate the outer velocity is constant, in the channel u(x) must increase as δ(x) increases. Show that, for profile (2) in the shear layers and v_x = u(x) in the core, 

A somewhat lengthy calculation that takes this into account (which you are not asked to reproduce) yields a = 0.052 (Deen, 2012, p. 287). For comparison, if x = L_E is considered to be where the velocity change at the channel center is 99% complete, a numerical solution of the Navier–Stokes equation gives a = 0.088 (Atkinson et al., 1969). The discrepancy between the integral-momentum and numerical results is less than it might seem, as a = 0.052 actually corresponds to about 93% of the velocity change and the precise percentage used to define L_E is arbitrary.

Transcribed Image Text:

ty X x=0 Core Shear Layer 0